In vielen realen Anwendungen sind Zusammenhänge zwischen Variablen nichtlinear. Klassische lineare Regressionsmodelle können solche Zusammenhänge nicht adäquat erfassen. Trotzdem gibt es auch in linearen Regressionsmodellen Techniken zur Modellierung nichtlinearer Zusammenhänge.
Polynomiale Regression
Konzept
Polynomfunktionen sind eine einfache Methode zur Approximation nichtlinearer Zusammenhänge. Die Idee ist, eine lineare Regression nicht auf die Originaldaten, sondern auf transformierte Variablen anzuwenden. Dabei werden die Formel der linearen Funktion so angepasst, dass auch nichtlineare Zusammenhänge erfasst werden können. Ein Polynom n-ter Grades hat die Form
mathjax
\(f(x)=a_nx^n+a_{n−1}x^{n−1}+⋯+a_1x+a_0\)Die zu schätzenden Koeffizienten sind a0, a1, …, an bestimmen die Form der Kurve. Je höher der Grad n, desto flexibler ist das Modell. Allerdings kann ein zu hoher Grad zu Overfitting führen, sodass das Modell zwar die Trainingsdaten gut beschreibt, aber schlecht auf neue Daten verallgemeinert.
Polynomiale Regression eignet sich gut, wenn Daten eine glatte, aber nichtlineare Struktur aufweisen. Beispiele sind Wachstumsraten (z.B. wirtschaftliche Trends) oder Wachstumskurven (z.B. bei medizinischen Messwerten).
Beispiel in Python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
# Beispieldaten generieren
np.random.seed(0)
x = np.linspace(1, 10, 100).reshape(-1, 1)
# Beispielhaftes kubisches Polynom: f(x) = 1*x^3 - 2*x^2 + 3*x + 5 + Rauschen
y = 1 * x.flatten()**3 - 2 * x.flatten()**2 + 3 * x.flatten() + 5 + np.random.normal(0, 10, size=x.shape[0])
# Erzeugen von Polynomfeatures (hier Grad 3)
poly = PolynomialFeatures(degree=3)
x_poly = poly.fit_transform(x)
# Lineare Regression auf den polynomisierten Daten
model = LinearRegression()
model.fit(x_poly, y)
y_poly_pred = model.predict(x_poly)
# Visualisierung
plt.figure(figsize=(8, 4))
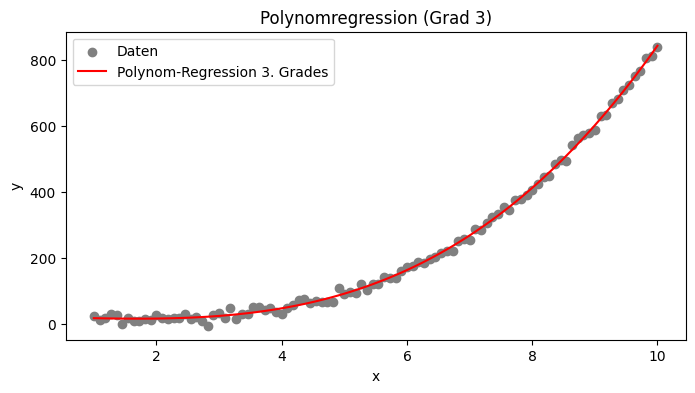
plt.scatter(x, y, label='Daten', color='gray')
plt.plot(x, y_poly_pred, label='Polynom-Regression 3. Grades', color='red')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Polynomregression (Grad 3)')
plt.legend()
plt.show()
Splines
Konzept
Splines unterteilen den Wertebereich in Intervalle, innerhalb derer einzelne niedriggradige Polynome definiert werden. Besonders beliebt sind kubische Splines, die sich folgendermaßen darstellen lassen:
\(S_i(x)=a_i+b_i(x−x_i)+c_i(x−x_i)^2+d_i(x−x_i)^3\)Die einzelnen Polynome werden an den Knotenpunkten (xi) so verbunden, dass die Funktion an diesen Stellen stetig ist. Dadurch wird eine hohe Flexibilität erreicht, ohne zu großes Overfitting-Risiko.
Beispiel in Python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import SplineTransformer
# 1. Daten generieren
np.random.seed(42)
x = np.sort(np.random.rand(100)) # 100 zufällige Punkte zwischen 0 und 1, sortiert
y = np.sin(2 * np.pi * x) + np.random.normal(0, 0.1, x.shape[0]) # Sinusfunktion + Rauschen
x = x.reshape(-1, 1) # Umformen in ein 2D-Array, wie es scikit-learn erwartet
# 2. Spline-Transformation
# Hier wird die Eingangsvariable in eine Basis von Splines transformiert.
# Wir verwenden n_knots=5, was zu 5 Knotenpunkten führt, und den Standardgrad 3 (kubische Splines).
spline_transformer = SplineTransformer(n_knots=5, degree=3, include_bias=False)
X_spline = spline_transformer.fit_transform(x)
# 3. Modell schätzen: Lineare Regression auf den Spline-Features
model = LinearRegression()
model.fit(X_spline, y)
y_pred = model.predict(X_spline)
# 4. Ergebnisse visualisieren
plt.figure(figsize=(8, 4))
plt.scatter(x, y, label='Daten', color='gray')
plt.plot(x, y_pred, label='Spline Regression', color='red')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Regression mit Splines (kubisch)')
plt.legend()
plt.show()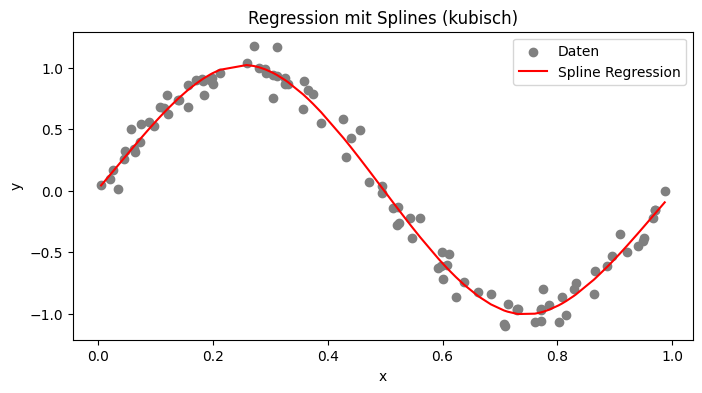
Logarithmische Transformationen
Viele nichtlineare Zusammenhänge lassen sich durch logarithmische Transformationen linearisieren. Es gibt zwei gängige Varianten: Log-Log-Transformation und Log-Level Transformation.
Log-Log-Transformation
Betrachten wir den Fall, dass ein Potenzgesetz vorliegt:
\(y=a \cdot x^b\)Durch Logarithmieren beider Seiten erhalten wir:
\(log(y)=log(a)+b⋅log(x)\)Dadurch wird der Zusammenhang linear und man kann b mit einer linearen Regression schätzen.
Die Steigung b zeigt die prozentuale Änderung von y in Reaktion auf eine prozentuale Änderung von x.
Beispiel in Python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# Beispieldaten generieren
np.random.seed(0)
x = np.linspace(1, 10, 50) # x-Werte von 1 bis 10
# Potenzgesetz: y = 2 * x^3 plus Rauschen, angepasst um immer positive y zu erhalten
y = 2 * x**3 + np.random.normal(50, 10, size=x.shape)
# Logarithmieren von x und y
log_x = np.log(x).reshape(-1, 1)
log_y = np.log(y)
# Lineare Regression auf den logarithmierten Daten
model_loglog = LinearRegression()
model_loglog.fit(log_x, log_y)
log_y_pred = model_loglog.predict(log_x)
# Rücktransformation zur Darstellung im Originalraum (optional)
y_pred = np.exp(log_y_pred)
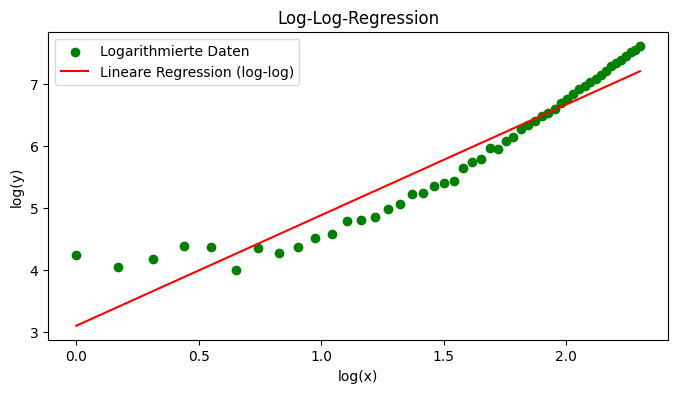
# Visualisierung im Log-Log-Raum
plt.figure(figsize=(8, 4))
plt.scatter(log_x, log_y, label='Logarithmierte Daten', color='green')
plt.plot(log_x, log_y_pred, label='Lineare Regression (log-log)', color='red')
plt.xlabel('log(x)')
plt.ylabel('log(y)')
plt.title('Log-Log-Regression')
plt.legend()
plt.show()
# Ausgabe der Modellparameter
print("Log-Log Modell:")
print("Geschätzter Interzept (log(a)):", model_loglog.intercept_)
print("Geschätzte Steigung (b):", model_loglog.coef_[0])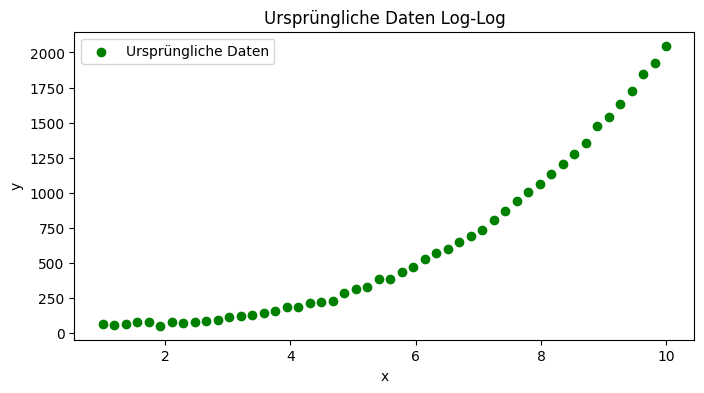
Log-Level Transformation
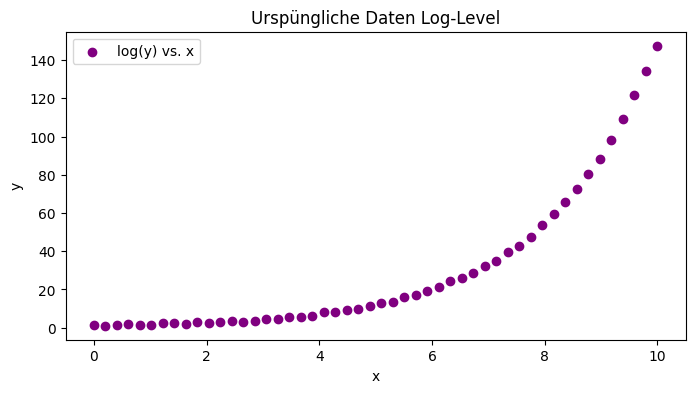
Die Log-Level Transformation wird verwendet wenn ein exponentielles Wachstum vorliegt. Hierbei wird nur eine der Variablen transformiert:
\(y=a \cdot x^{bx}\)Durch Logarithmieren von y erhalten wir:
[/latex]log(y)=log(a)+b \cdot x[/latex]
Dies ermöglicht es, mittels linearer Regression den Parameter b zu schätzen. Die Steigung b zeigt, wie stark y in Bezug auf x wächst, wobei ein Anstieg um eine Einheit in x zu einer Multiplikation von y mit eb führt.
Beispiel in Python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# Beispieldaten generieren
np.random.seed(42)
x_exp = np.linspace(0, 10, 50) # x-Werte von 0 bis 10
# Exponentielles Wachstum: y = 1 * exp(0.5 * x) plus Rauschen
y_exp = 1 * np.exp(0.5 * x_exp) + np.random.normal(0, 0.5, size=x_exp.shape)
# Logarithmieren von y
log_y_exp = np.log(y_exp)
# Lineare Regression: x bleibt unverändert, log(y) ist Zielvariable
model_loglevel = LinearRegression()
model_loglevel.fit(x_exp.reshape(-1, 1), log_y_exp)
log_y_exp_pred = model_loglevel.predict(x_exp.reshape(-1, 1))
# Rücktransformation zur Darstellung im Originalraum (optional)
y_exp_pred = np.exp(log_y_exp_pred)
# Visualisierung: Plot der logarithmierten Zielvariablen
plt.figure(figsize=(8, 4))
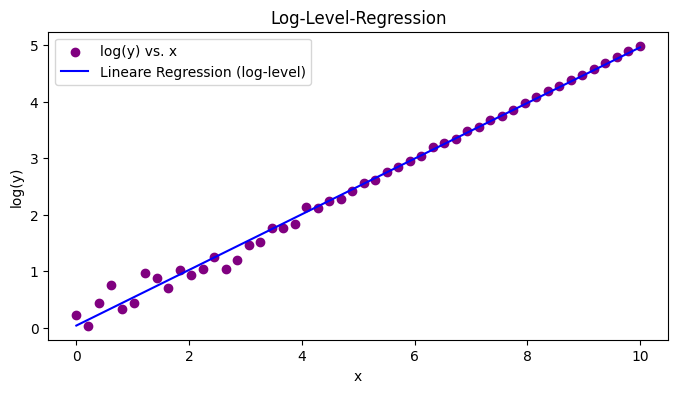
plt.scatter(x_exp, log_y_exp, label='log(y) vs. x', color='purple')
plt.plot(x_exp, log_y_exp_pred, label='Lineare Regression (log-level)', color='blue')
plt.xlabel('x')
plt.ylabel('log(y)')
plt.title('Log-Level-Regression')
plt.legend()
plt.show()
# Ausgabe der Modellparameter
print("Log-Level Modell:")
print("Geschätzter Interzept (log(a)):", model_loglevel.intercept_)
print("Geschätzte Steigung (b):", model_loglevel.coef_[0])