PYMC
Um Bayesianische Methoden zu nutzen, benötigt man PYMC. Die offizielle Dokumentation dazu findet sich hier: https://www.pymc.io/welcome.html
Die Installation unter Windows ist sehr kompliziert, deshalb verwende ich hierfür Linux unter Windows mit WSL.
Details zur Installation unter Windows findet ihr hier:
Oder hier: https://awhug.github.io/2020-07-10-installing-pymc3-and-theano-on-windows-10-with-wsl/
Am einfachsten ist die Installation unter WSL, indem man ein vorgefertigtes Conda-Environment verwendet:
conda create -c conda-forge -n pymc_env "pymc>=5"
conda activate pymc_envUm in VSCode zu arbeiten, reicht es, wenn man das Environment von WSL aus aktiviert, in seinen Projektordner wechselt und dann diesen Befehl eingibt:
code .Bayesianische Regression
Bayesianische Regressionsmodelle erweitern die klassische Regression, indem sie Wahrscheinlichkeitsverteilungen für die Modellparameter verwenden. Anstatt einzelne Punktwerte für die Parameter zu schätzen, berechnet die bayesianische Methode Wahrscheinlichkeitsverteilungen für diese Werte.
Um diesen Ansatz zu verstehen, berechnen wir zunächst eine einfache lineare Regression mit generierten Daten. Die Daten basieren auf einer linearen Funktion mit einer Steigung von 2,5 und einem Achsenabschnitt von 1, wobei zusätzliches Rauschen die Werte zufällig streut:
# Daten generieren
X = np.linspace(0, 10, 50)
wahre_slope = 2.5
wahre_intercept = 1.0
rauschen = np.random.normal(scale=1.0, size=X.shape)
Y = wahre_slope * X + wahre_intercept + rauschenDas Ganze sieht dann so aus:
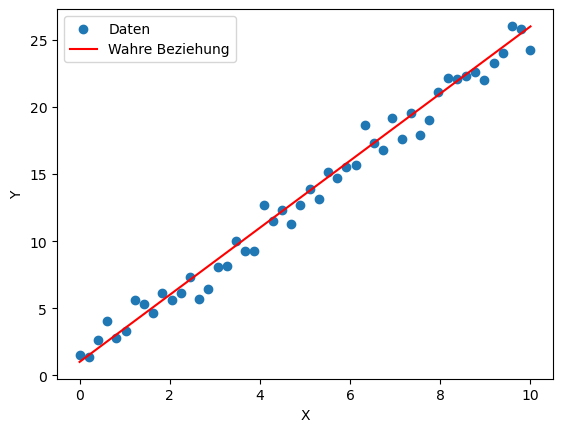
Wir definieren nun ein bayesianisches Modell, bei dem die Steigung (slope) und der Achsenabschnitt (intercept) normalverteilt sind. Das Rauschen (sigma) wird als Half-Normal-Verteilung angenommen.
Um das Bayesianische Modell zu definieren gehen wir nun davon aus, dass sich der wahre Wert für den Achsenabschnitt und für die Steigung mit einer zu ermittelnden Wahrscheinlichkeit in einem bestimmten Bereich befindet. D.h. wir gehen nicht davon aus, dass wir den wahren Wert für diese Paramter ermitteln werden, sondern ermitteln stattdessen „nur“ die Wahrscheinlichkeit mit der sich der Wert der Parameter in einem bestimmten Bereich befindet. Um diese Bereich zu ermitteln gehen wir davon aus, dass die Werte der beiden Parameter normalverteilt sind.
Das gleichen Ansatz verwenden wir auch für das Rauschen (=Sigma). Hier gehen wir allerdings von einer HalfNormal-Verteilung aus:
intercept = pm.Normal("intercept", mu=0, sigma=10)
slope = pm.Normal("slope", mu=0, sigma=10)
sigma = pm.HalfNormal("sigma", sigma=1)Wenn wir nun das Regressionmodell definieren, so sieht dieses zunächst genauso aus wie in der klassischen Statistik. Nur dass sich hinter den einzelnen Variablen nicht mehr feste Werte befinden, sondern nun Wahrscheinlichkeitsverteilungen:
mu = intercept + slope * XErmitteln wollen wir nun also das Likelihood. Für jeden Wert der beiden Parameter „intercept“ und „slope“ ist dies die Wahrscheinlichkeit, die Daten X und Y zu erhalten.
# Likelihood
Y_obs = pm.Normal("Y_obs", mu=mu, sigma=sigma, observed=Y)Durchgeführt wird die Analyse mittels Markov Chain Monte Carlo Sampling (MCMC). MCMC ist ein Verfahren zur Approximation der Posterior-Verteilung durch Stichproben. Der Algorithmus beginnt mit zufälligen Startwerten für die Modellparameter und durchläuft dann eine große Anzahl von Iterationen, in denen er neue Werte für die Parameter vorschlägt. Diese neuen Werte werden basierend auf ihrer Wahrscheinlichkeit entweder angenommen oder verworfen. Durch viele Iterationen nähert sich die Verteilung der Parameter ihrer tatsächlichen Posterior-Verteilung an.
In unserem Fall nutzt PyMC den NUTS-Sampler (No-U-Turn Sampler), eine Variante der Hamiltonian Monte Carlo (HMC) Methode. Dieser Sampler ist besonders effizient und benötigt keine manuelle Anpassung der Schrittweiten wie bei einfachen Metropolis-Hastings-Samplern.
Das Sampling liefert eine große Anzahl an Stichproben für die Parameterverteilungen, die anschließend analysiert werden können.
# Inferenz mittels MCMC Sampling
trace = pm.sample(2000, tune=1000, cores=2, target_accept=0.9)Hier nochmal die komplette Modelldefinition mit PYMC:
# Bayesianisches Modell definieren
with pm.Model() as bayes_model:
# Priors für die Parameter
intercept = pm.Normal("intercept", mu=0, sigma=10)
slope = pm.Normal("slope", mu=0, sigma=10)
sigma = pm.HalfNormal("sigma", sigma=1)
# Lineares Modell
mu = intercept + slope * X
# Likelihood
Y_obs = pm.Normal("Y_obs", mu=mu, sigma=sigma, observed=Y)
# Inferenz mittels MCMC Sampling
trace = pm.sample(2000, tune=1000, cores=2, target_accept=0.9)Die Ergebnisse der Modellberechnung können mit Arviz visualisiert werden.
import arviz as az
az.plot_trace(trace)
plt.show()Links sieht man die Verteilung der geschätzen Parameter „Intercept“, „Slope“ und „Sigma“. Rechts sind die Parameterwerte für die einzelnen Iterationen des MCMC-Samplings dargestellt.
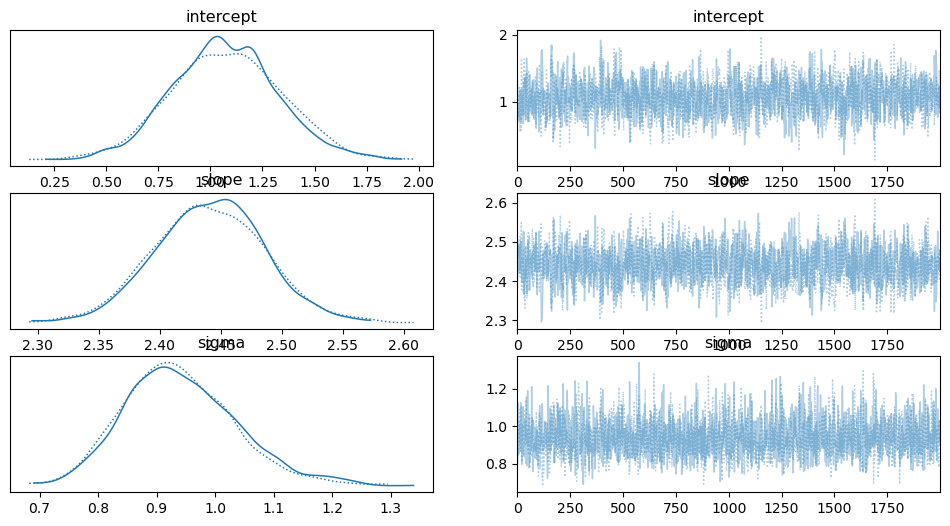
Die berechneten Werte für die Parameter sind:
| Parameter | Mittelwert | 95%-Intervall |
|---|---|---|
| Intercept | 1.07 | [0.60, 1.61] |
| Slope | 2.44 | [2.36, 2.53] |
| Sigma | 0.94 | [0.75, 1.12] |
Das bedeutet, dass der wahre Wert der Steigung mit einer Wahrscheinlichkeit von 95 % im Bereich zwischen 2.36 und 2.53 liegt.
Vorhersagen von neuen Werten
Genau wie in der klassischen Regression kann man auch in der Bayesianischen Regression neue Werte vorhersagen. Hierbei ziehen wir neue Stichproben für die vorhergesagten Werte Y_obs, basierend auf den Posterior-Verteilungen der Modellparameter. Dies ermöglicht eine robuste Schätzung der Werte für neue Eingaben und reflektiert gleichzeitig die Unsicherheit in den Parametern. Dabei nutzen wir das posterior-prädiktive Sampling:
In PYMC geht das so:
# Neue X-Werte für Vorhersagen
X_new = np.linspace(0, 10, 100)
# Posterior-Prädiktive Stichproben ziehen
with bayes_model:
posterior_pred = pm.sample_posterior_predictive(trace)
# Extrahiere die Parameterproben
intercept_samples = trace.posterior["intercept"].values.flatten()
slope_samples = trace.posterior["slope"].values.flatten()
# Berechnung der vorhergesagten Werte
Y_preds = np.mean(intercept_samples) + np.mean(slope_samples) * X_newIm Gegensatz zu klassischen Regression wird bei der Bayesianische Regression die Unsicherheit der Parameter also explizit modelliert. Der Vorteil der Bayesianischen Regression
- Berücksichtigung der Unsicherheit: Anstatt nur Punktwerte für Parameter zu berechnen, erhalten wir Verteilungen, die die Unsicherheit der Schätzungen widerspiegeln.
- Flexible Modellierung: Man kann Vorwissen über die Parameter (Priors) in die Analyse einfließen lassen.
- Natürliche Interpretation: Wahrscheinlichkeiten ermöglichen intuitive Aussagen über Parameterbereiche.



