In vielen Machine Learning Modellen wird zum Optimieren der Parameter das Gradientenabsteigsverfahren angewendet. Besonders bei neuronalen Netzen ist dieses Verfahren ein wichtiger Standard. Aber auch in einfacheren Modellen wie der linearen Regression findet es Anwendung. In diesem Beitrag wird Schritt für Schritt erklärt, wie das Verfahren funktioniert.
Einfache lineare Regression
Um das Verfahren besser zu verstehen, beginnen wir mit einem einfachen Beispiel: einer linearen Regression mit nur einer unabhängigen Variable. Unser Ziel ist es, den Einfluss von auf zu schätzen.
Angenommen, wir haben drei Datenpunkte:
\(P_1(2,3), P_1(4,4), P_3(6,7)\)In einem Koordininatensystem lassen sich diese drei Punkte so darstellen:
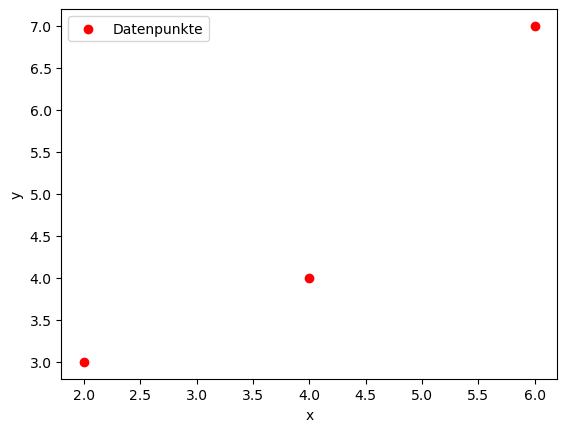
Unsere Aufgabe ist es, eine gerade Linie durch diese Punkte zu legen. Die allgemeine Form einer linearen Funktion lautet:
\(y=mx+t\)Wobei m die Steigung und y der Achsenabschnitt ist.
Kostenfunktion
Zunächst müssen wir festlegen, wie wir unsere Gerade optimieren wollen. Wie benötigen also eine Methode um zu bewerten wie gut eine gegebene Linie zu den Daten passt. Zu diesem Zweck definieren wir eine Kostenfunktion (oder Fehlerschätzfunktion). Diese Funktion misst, wie weit die vorhergesagten Werte von den tatsächlichen Werten entfernt sind.
Die häufig verwendete Kostenfunktion ist der mittlere quadratische Fehler (Mean Squared Error, MSE). Man berechnet also für jeden Punkt, die Abweichung der Schätzung (festgelegt durch unsere Regressionsgerade) vom realen Wert. Die Summe aller Abweichungen teilt man durch die Anzahl an Trainingsbeispielen.Durch die Quadrierung der Abweichung werden einerseits negative und positive Abweichungen gleich bewertet und gleichzeitig fallen größere Abweichungen stärker in Gewicht.
\(J(m,t) = \frac{1}{n} \sum\limits_{i=1}^n (y_i-(mx_i + t))^2\)Gradienten
Gradientenabstieg heißt nun, dass wir versuchen diese Kostenfunktion zu minimieren indem wir die Parameter unserer Regressionsgerade entsprechen anpassen. Diese Parameter sind:
- m (die Steigung der Geraden) und
- t (der Achsenabschnitt)
Um die die Paramter zu optimeren, benötigen wir eine Möglichkeit die Steigung in Abhängigkeit der Parameter zu berechnen. Dafür benötigen wir die partiellen Ableitungen (= Gradient) der Kostenfunktion nach m und t. Ein Gradient gibt die Richtung der steilsten Änderung einer Funktion an. In unserem Fall beschreibt der Gradient, wie sich die Kostenfunktion verändert, wenn die Werte der Parameter leicht verändert werden. Da es sich um eine partielle Ableitung handelt, kann man damit ermitteln welchen Einflss ein einzelner Paramter auf den Gesamtfehler hat, währen der andere Paramter konstant bleibt.
Hier die partielle Ableitung nach m:
\(\frac {\partial J}{\partial m} = \frac{2}{n} \sum_{i=1}^{n}(x_i(y_i-(mx_i + t))\)Wer sich fragt, wie die partielle Ableitung aus der Kostenfunktion bestimmt wurde: Hier kommt die Kettenregel zum Einsatz. Wir berechnen erst die äußere Ableitung (die hoch 2 wird nach vorne gezogen) und danach multiplizieren wir das Ergebnis mit der inneren Ableitung nach m (das ist einfach xi).
Der Gradient der Kostenfunktion abgeleitet nach t sieht dann so aus:
\(\frac {\partial J}{\partial t} = \frac{2}{n} \sum_{i=1}^{n}(y_i-(mx_i + t))\)Wir starten nun mit zufällig gesetzten Werten für m und t und berechnen für jeden unserer drei Punkt die Steigung der Funktion. Dann verändern wir die Werte in umgekehrter Richtung der Steigung, bewegen uns also entlang der „Steigung herunter“ (daher „Gradientenabstieg“).
Schrittweise Optimierung der Parameter
1. Initialisierung
Wie setzen m und t auf einen Startwert (bspw. 0)
2. Gradienten berechnen
Wir setzen unsere Datenpunkte in die Ableitung ein. Für den Parameter m sieht das so aus:
\( \frac {\partial J}{\partial m} = – \frac{2}{3}(2\cdot (3-(0\cdot2+0)) + (2\cdot (4-(0\cdot4+0)) +(6\cdot (7-(0\cdot6+0)) = -42.666\)Für den Parameter t sieht das so aus:
\( \frac {\partial J}{\partial m} = – \frac{2}{3}((3-(0\cdot2+0)) + ((4-(0\cdot4+0)) +((7-(0\cdot6+0)) = -9.333\)3. Parameter anpassen
Nun passen wir die Werte für m und t an. Dabei gehen wir mithilfe einer Lernrate alpha schrittweise vor. Das bedeutet, dass wir in jeder Iteration jeweils nur eine kleine Anpassung der Paramter vornehmen und uns damit Schritt für Schritt dem optimalen Wert annähern. In diesem Beispiel setzen wir die Lernrate auf 0.01.
Die neuen Werte lauten dann :
\(m = m – (0.01 \cdot (-42.666) ) = 0,42666 \) \(t = t- (0.01 * (-9.333) ) = 0,09333\)4. Wiederholen
Dieses Verfahren wird in mehreren Iterationen durchlaufen (Epochen), bis die Kostenfunktion minimiert ist.
Pythoncode
In Python lässt sich dieses Beispiel sehr gut selbst nachrechnen:
# Beispiel-Datenpunkte
x = np.array([2, 4, 6])
y = np.array([3, 4, 7])
# Hyperparameter
alpha = 0.01 # Lernrate
epochs = 100 # Anzahl der Iterationen
# Initialisierung von m und t
m = 0.0
t = 0.0
# Verlauf speichern
history = []
# Gradientenabstieg
for _ in range(epochs):
y_pred = m * x + t # Vorhersagen
error = y - y_pred # Fehler
# Gradienten berechnen
dm = -2 / len(x) * np.sum(x * error)
dt = -2 / len(x) * np.sum(error)
# Parameter aktualisieren
m -= alpha * dm
t -= alpha * dt
# Kosten berechnen und speichern
cost = np.mean(error**2)
history.append((m, t, cost))
# Endgültige Werte
print(f'Finale Werte: m = {m:.4f}, t = {t:.4f}')Das Ergebnis der Optimierung sieht dann so aus:
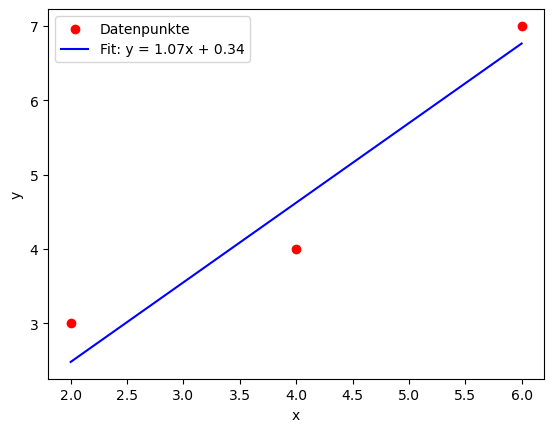
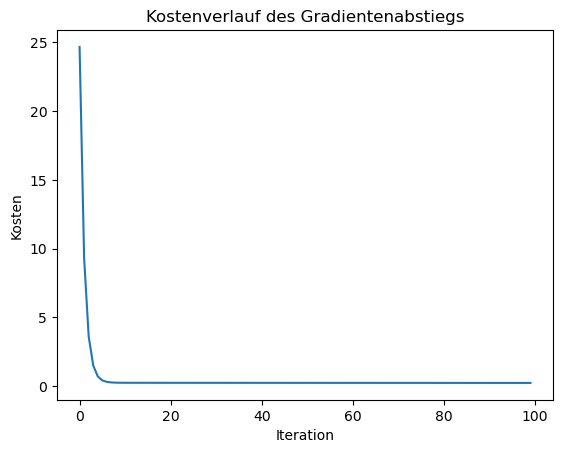
Die in der History gespeicherten Werte können verwendet werden um den Verlauf des Gradientenabstiegs zu plotten. Dabei zeigt sich, dass in diesem Fall bereits nach wenigen Epochen ein idealer Wert erreicht wird:
Multiple Regression
Das Verfahren lässt sich nun ebenso auch auf eine Regression mit mehreren Parametern anwenden, beispielsweise einer multiplen linearen Regression mit zwei unabhängigen Variablen x1 und x2. Die Funktion hat drei Parameter. Theta0 ist der Bias Term bzw. der Achsenabschnitt. Theta1 und Theta2 sind die Gewichte für die beiden Variablen x1 und x2.
\(h_\theta(x_1,x_2)=\theta_0 + \theta_1 x_1 + \theta_2 x_2\)Als Kostenfunktion verwenden wir auch hier den Mean Squared Error (MSE), also die mittlere quadratische Abweichung. Auch hier wird für jeden Datenpunkt i jeweils die Differenz zwischen Vorhersage und realem Wert berechnet. Die Summe aller Abweichungen teilt man durch die Anzahl an Trainingsbeispielen.
\(J(\theta_0,\theta_1,\theta_2) = \frac{1}{2m} \sum_{i=1}^m (h_\theta (x_1^i, x_2^i)-y^i)^2\)Die Gradienten sind nun die partiellen Ableitungen dieser Kostenfunktion J nach allen drei Parametern.
Gradient nach theta0:
\(\frac {\partial J}{\partial \theta_0} = \frac{1}{m} \sum_{i=1}^{m}(h_\theta (x_1^i, x_2^i)-y^i)\)Gradient nach theta1:
\(\frac {\partial J}{\partial \theta_1} = \frac{1}{m} \sum_{i=1}^{m}((h_\theta (x_1^i, x_2^i)-y^i) \cdot x_1 ^i)\)Gradient nach theta2:
\(\frac {\partial J}{\partial \theta_2} = \frac{1}{m} \sum_{i=1}^{m}((h_\theta (x_1^i, x_2^i)-y^i) \cdot x_2 ^i)\)Die Berechnung erfolgt nun genauso wie im Fall der einfachen linearen Regression und lässt sich dementsprechend auch in Python fast genauso implementieren:
# Beispiel-Datenpunkte
x1 = np.array([2, 4, 6])
x2 = np.array([1, 8, 17])
y = np.array([3, 6, 7])
# Hyperparameter
alpha = 0.001 # Lernrate
epochs = 100 # Anzahl der Iterationen
# Initialisierung von m und t
theta0 = 0.0
theta1 = 0.0
theta2 = 0.0
for _ in range(epochs):
# Vorhersagen berechnen
y_pred = theta0 + theta1 * x1 + theta2 * x2
error = y - y_pred # Fehler
# Gradienten berechnen
dtheta0 = -2/m * np.sum(error) # Gradient für theta0 (Bias)
dtheta1 = -2/m * np.sum(error * x1) # Gradient für theta1
dtheta2 = -2/m * np.sum(error * x2) # Gradient für theta2
# Parameter aktualisieren
theta0 -= alpha * dtheta0
theta1 -= alpha * dtheta1
theta2 -= alpha * dtheta2
# Kosten berechnen und speichern
cost = np.mean(error**2)
history.append((theta0, theta1, theta2, cost))Wer genau hinsieht, wird feststellen, dass die Lernrate gegenüber dem ersten Beispiel reduziert wurde. Der Grund dafür ist, dass die Werte bei höherer Lernrate nicht konvergieren, also keine stabilen Werte für die Parameter ergeben. Durch die Reduzierung der Lernrate kann dieses Problem behoben werden. Ähnlich ist es auch bei tatsächlicher Anwendung des Gradientenabstiegs in der Praxis teilweise notwendig die Lernrate an die zu optimierende Funktion anzupassen.
Neuronale Netzerke / Perzeptron
Bekannt ist das Gradientenabstiegsverfahren natürlich vor allem für die Anwendung bei neuronalen Netzen. Zusätzlich wird hier noch der Backpropagation-Algorithmus angewendet. Der Pythoncode für die Anwendung des Gradientenabstiegs bei neuronales Netz findet ihr hier.



