Explainable A.I. – SHAP

Grundidee

SHAP (SHapey Additive exPlanations) messen den Beitrag von Features zur Gesamtvorhersage in Machine-Learning-Modellen. Sie basieren auf der Spieltheorie und messen dort den fairen Beitrag jedes Spielers zu einem gemeinsamen Ergebnis in einem Kooperationsspiel.
Im Machine Learning wird jedes Feature als Spieler betractet. Der Beitrag eines Features wird durch die Veränderung der Modellvorhersage gemessen, wenn das Feature hinzugefügt wird. Die Shapley-Werte so verteilt, dass sie den fairen Beitrag jedes Features ermitteln.

Die offizielle Dokumentation findet sich hier.

Berechnung

1. Koalitionen bilden
   Es werden Koaltionen gebildet. Das sind alle möglichen Kombinationen der Features, also alle Kombinationen mit nur einem Feature, mit zwei Features usw.
   Das Modell wird dabei jeweils zweimal berechnet

• Einmal ohne das Feature xi
• Einmal mit dem Feature xi

1. Marginaler Beitrag
   Der marginale Beitrag ist einfach das Ergebnis der Vorhersage mit und ohne das Feature xi.
2. Durchschnittliche marginale Beitrag aus allen Koaltionen ergibt den Shapley-Wert. Dieser wird dabei als gewichtetes Mittel der marginalen Beiträge berechnet.
   Gewichtet wird dabei so, dass alle Koaltionen gleichmäßig berücksichtigt werden.

Beispiel bei drei Features:
Für jedes Feature (z. B. x1​) wird der marginale Beitrag berechnet, indem man es zu jeder möglichen Koalition, die x1​ nicht enthält, hinzufügt. Es gibt 2^(n-1) mögliche Koaltionen.

Beispiel für x1:

• Koalition: S={} → Beitrag: f(S∪{x1}) − f(S)
• Koalition: S={x2} → Beitrag: f(S∪{x1}) − f(S)
• Koalition: S={x3}} → Beitrag: f(S∪{x1}) − f(S)
• Koalition: S={x2,x3} → Beitrag: f(S∪{x1}) − f(S)

Die Gewichtung wird so berechnet:
S!-(n-|S|-1)! / (n!)

Das ist so zu interpretieren:

• S! ist die Anzahl der Features die ohne xi in der Koaltion enthalten sind (bzw. davon jeweils die Permutation, also wie viel Kombinationen es gibt). In der ersten Koaltion S{} also 0. In der zweiten Koaltion S={x2} also 1 usw.
• (n-|S|-1)! ist die Anzahl der Features die nicht enthalten sind (bzw. davon jeweils die Permutation, also wie viel Kombinationen es gibt). In der ersten Koaltion S{} also 2 (nämlich x2 und x3). In der zweiten Koaltion S={x2} also 1 (nämlich x3) usw.
• n! ist die Gesamtzahl der Permutationen aller n Features

Dadurch wird so gewichtet, dass jede Ebene von Koalitionen mit dem gleichen Gesamtgewicht eingeht. Hier also:

• Koalition: S={} → Gewicht 1/6
• Koalition: S={x2} → Gewicht 1/6
• Koalition: S={x3}} → Gewicht 1/6
• Koalition: S={x2,x3} → Gewicht: 1/3

In Python

pip install shap
# Conda:
conda install shap

pip install shap
# Conda:
conda install shap

Zunächst trainieren wir ein einfaches Modell. Hier wirder mit dem bekannten Iris-Datensatz.

import shap
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris

# 1. Datensatz laden
data = load_iris()
X = pd.DataFrame(data.data, columns=data.feature_names)
y = data.target

# 2. Datensatz in Trainings- und Testdaten aufteilen
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 3. Modell trainieren
model = RandomForestClassifier(random_state=42)
model.fit(X_train, y_train)

import shap
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris

# 1. Datensatz laden
data = load_iris()
X = pd.DataFrame(data.data, columns=data.feature_names)
y = data.target

# 2. Datensatz in Trainings- und Testdaten aufteilen
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 3. Modell trainieren
model = RandomForestClassifier(random_state=42)
model.fit(X_train, y_train)

Da es sich hier um einen RandomForestClassifier handelt benötigt man aus SHAP den TreeExplainer:

# 4. SHAP-Erklärungen erstellen
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X_test)

# 5. Visualisierung
shap.summary_plot(shap_values, X_test)

# 4. SHAP-Erklärungen erstellen
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X_test)

# 5. Visualisierung
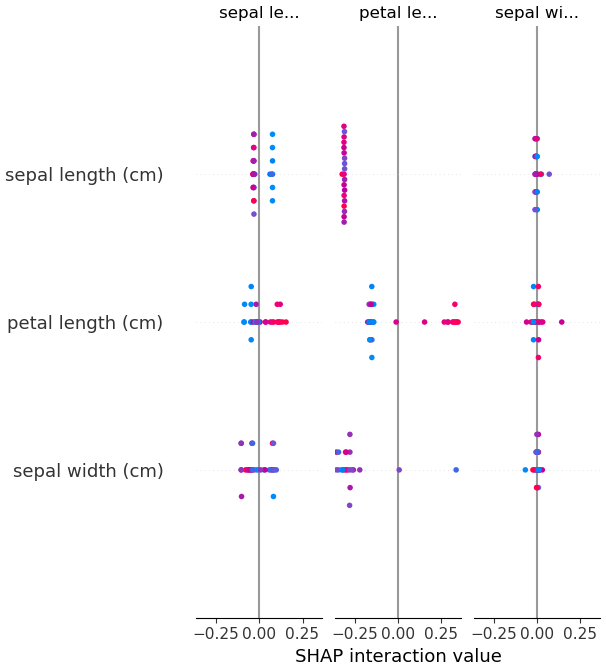
shap.summary_plot(shap_values, X_test)

Der SHAP Summary Plot zeigt nun den Einfluss der Features auf die Modellvorhersage. Jede Zeile entspricht einem Feature, jeder Punkt repräsentiert eine Instanz. Die Farbe zeigt den Feature Wert an, blau = niedrig, rot = hoch.

Die X-Achse zeigt nun den Einfluss. Je weiter ein Punkt links oder rechts liegt, desto größer ist sein Einfluss. Je weiter rechts ein Punkt liegt, um so mehr erhöht sich die Modellvorhersage, je weiter links er linkt um so mehr senkt sich die Modellvorhersage.

Bei Klassenvorhersagen bedeutet das: Ein positiver SHAP-Wert bedeutet dass das Feature die Vorhersage in Richtung einer höhere Klassenzugehörigkeit schiebt.